| Chaos Theory, Data Mining and World Adventure (1998-2003) |
|
In July 1998, I joined the Chemical Engineering department at The University of Tennessee, Knoxville (UTK) as a Graduate Research Assistant and direct Ph.D. student. My research focused on time series obtained from complex nonlinear dynamic systems. Most Chemical Engineering systems are highly complex and cannot be analytically modeled: that was the link. A quick look at the Navier-Stokes equations brings out the complexity. However, to mathematicians the equations might still appear totally sufficient and a Physicist might solve those equations with some assumptions that in their mind need no justification. To that audience, perhaps the highly destabilizing influence of dead time or lag time on the standard modeling approach via Laplace or Z-transforms. |
| Nonlinear Time Series Analysis and Research |
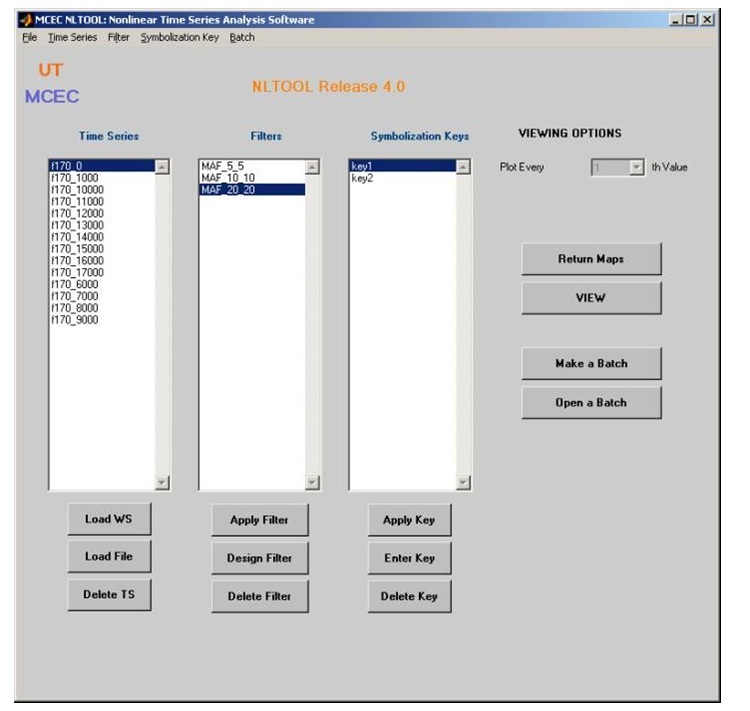
My research was largely funded by the Measurement and Control Engineering Center (MCEC), for the CANDIES (Control/Chaos and Nonlinear Dynamics for Industrial Engineering Systems) project. Acronyms matter in research! MCEC provided a forum for applied and practical research to solve technical problems in process control and optimization. Why Chemical Engineering? Many people do not know that there is a lot of math and physics and much less chemistry in that discipline. The most endearing and frustrating aspect of Chemical Engineering is the immense complexity of transport phenomena and thermodynamical modeling that requires much computational power and sophistication. As a result, one has to learn how to strike the right balance between empirical studies and explicit mathematical modeling. The often cited example of this trade-off is the Chilton-Colburn analogy that attempts to approximately modeling mass transfer (much harder to measure) with heat transfer (that could be measured much more precisely). A natural consequence of the complexity of processes studied in Chemical Engineering is the need to consider the interplay between opposing forces, such as the the momentum force of flow (that is kinetic) viscous forces (that are inertial): the dimensionless ratio of these two forces is the famous Reynolds number. The image on the left is the home screen of the nonlinear time series analysis GUI I built as part of the CANDIES project. In 1999, there were no books on MATLAB GUIs and creating a nltool-like tool was far from easy. |
| Fluidized Beds and Artificial Intelligence |
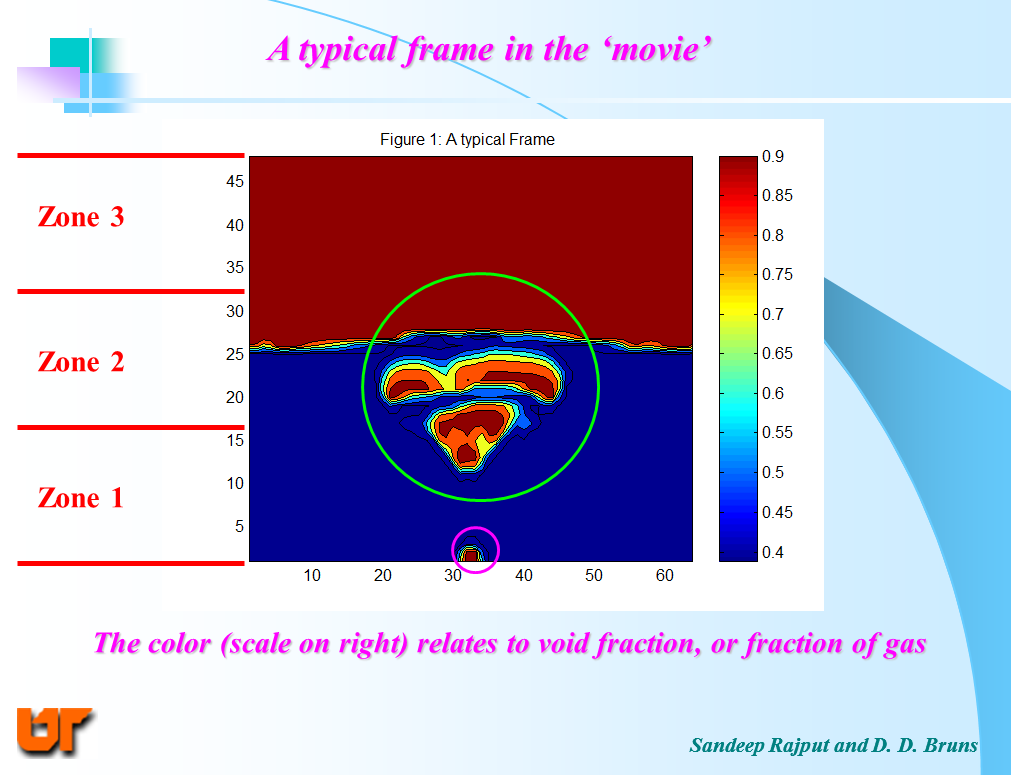
The image to the left shows one frame from a computational fluid dynamics (CFD) simulation, which was reduced to a monoscale image with the pixel value standing for the void fraction. Void fraction is a spatio-temporal property; at one time and in one place, void fraction is the fraction of the volume occupied by the fluid. MATLAB color-coded the image for better viewing, but it is essentially a matrix. The top third contains mostly fluid and does not change that much over time. For the conditions used, there is not much movement near walls either. Much action happens on the interface and along the jet of fluid funneling out to the interface. Every pixel here has its time series. We reduced the dimensionality of the data, which was 640 x 480 pixels every 200 milliseconds. At about 1.5 million values per second, it was a lot of data in 1999. Our challenge was to have a system that would work in production, so feature reduction was very important. With signal processing and machine learning techniques, we were able to train a Multilayer Perceptron (the most common sort of Neural Network) that did quite well for most cases. However, when the dynamics became chaotic, linear features extracted via Power Spectral density were not so predictive. Using mutual information and symbolization helped classification, but we still needed to use Fuzzy C-means clustering instead of the erstwhile K-means clustering to produce reasonable results. Non-stationarity of the process became very evident in this phase. This work illustrates the complexity faced by researchers in applying a wide set of toolbox to a complex problem that has a physical basis nonetheless. |
| Nonlinear Time Series Analysis and Symbolization |
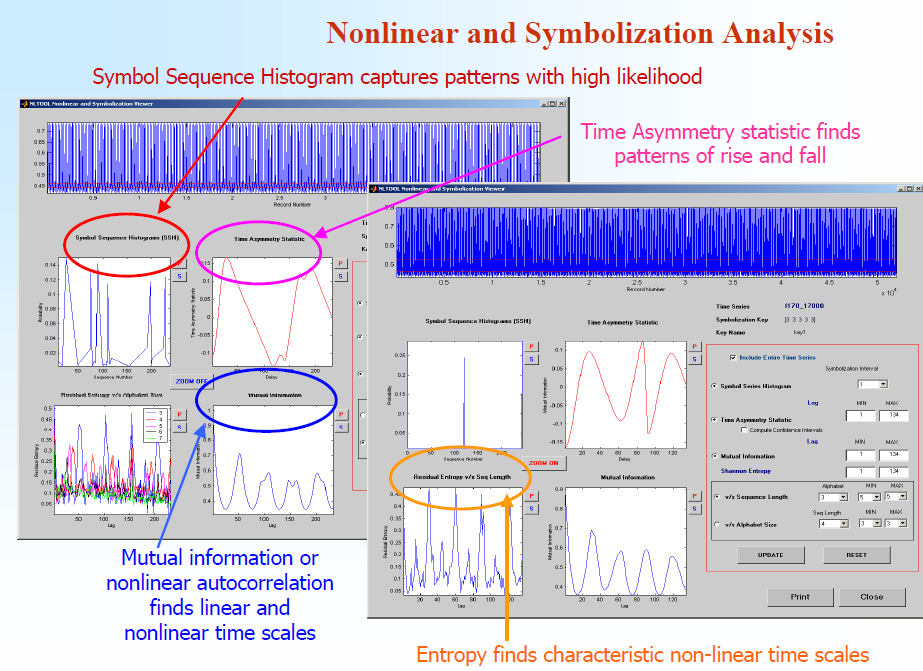
The image to the left shows the Symbolization viewer GUI created for discovering important timescales and nonlinearity in time series data. Symbolization can be thought of as coarse-graining the data. In the example, every measurement was reduced to one of three letters, through an equiprobable partition (cf. Alphabet size). From those letters one can form words of a fixed length (cf. sequence size). Together, this helps to reduce the noise, and for the right conditions at least, allows Takens' embedding theorem to hold and therefore be able to represent the dynamics. The only missing element here is the time-lag between the letters in forming words. All of this is highly similar to encoding of information via codes, of course. In some ways, this research appears out of place for Chemical Engineering but research has become very inter-disciplinary. Furthermore, some would argue that all measurements are nothing but a manifestation of information, some of it directly observable, some of it not so. The software package was licensed only to the MCEC member companies. We never did commercialize it and the last release was in 2002; we did hold a workshop for industry members to help them learn how to use the software and analyze time series data. |
| Lagniappe |
!['Butterfly' strange attractor from a gas-liquid bubble column [UT Knoxville & Oak Ridge National Lab] (1999-2004)](../img/bblcolattr.png)
In my five years at UT, I took courses ranging from 300-level French courses to 600-level Engineering courses in Electrical Engineering and Statistics. In particular, I was very interested in Control Systems, Pattern Recognition and AI. The latter two have remained familiar friends. It was a big change from the bustling megalopolis of Mumbai to the laid-back and idyllic East Tennessee. Delighted at not having to spend three hours every day commuting to work, I read voraciously, becoming a regular at the local used book stores. Along the way, I learned how to speak Spanish, as it turns out, with an Argentinian accent! Survived a trip to Paris (Paris, France, not Paris, Tennessee - home of world's biggest fish fry!) on a shoestring budget on the strength of my spoken French and the subtropical heat of Knoxville. I also started taking my cooking seriously, and began cooking foods from the world over- not least because I loved fine food but couldn't afford it as a graduate student. I joke that my fascination with world cuisines started at the local Sarku (a Japanese-themed fast food chain) run by Indonesians attending the local community college in the Southeastern US. Such is the nature of globalization! I passed my qualifying exams in Summer 2000 and finished my Ph.D. coursework in 2001. In the summer of 2002, I realized I had already taken many courses in Statistics and with a bit more effort could obtain a Master's degree, and I had found the applied focus of Statistics to my liking. My advisor was very generous and I was able to finish the coursework for everything by Spring 2003. I received my Ph.D. in Chemical Engineering officially in August 2003, and the M.S. in Statistics in December 2003. In 2003, a fellow alumnus, who at that time was working for Fair Isaac Corporation spoke to me about the cool things he was doing with payment card transaction data. I was impressed enough that I interviewed for the position, received an offer and accepted it, moving to Minneapolis in October 2003. |
| (c) Copyright 2013 Sandeep Rajput. All Rights Reserved. |